The School of Mathematics
We discovered that one possible way to find this square is to somehow halve the larger square into another square. Maybe we should try to halve each of the four small squares contained in the larger square.
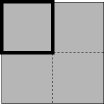
The light area has half the area of the small square. By doing the same for each of the four small square, in the right orientation, we find a square.
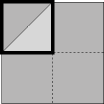
That's it! We have found a square that has precisely twice the area of the original square given to us. This method will work for any square -- just build a square on its diagonal, and that square will have twice the area of the original one.
We might ask some additional questions to extend the methods we have just devised:
- Can we generalize our result, by finding a square with other multiples of a given square? We have already seen how to find a square with four times the area of a given square. How about three or five? How about larger values? Might we find a general method? Perhaps only for some multiples?
- We might generalize in a different way -- instead of duplicating a square, which is basically adding a square to itself, we might want to add two non-identical squares. Given two squares, can you find a new square whose area is the area of the two squares combined?
The ideas that came up in the duplication of the square and in the thought behind these two questions give us some insight to the nature of area. Let us now return to our original question:
Main Question (Modified): When do two shapes have the same area? And when do two shapes not have the same area?
This is a difficult question in general, for example it is not at all obvious if these two shapes have the same area or not.

...but this question is easy to answer if the two shapes we are comparing are squares. For example, we can immediately see that these two squares don't have the same area -- since their side lengths are not equal.

So, one way we might solve the Main Question is by transforming each of the two shapes we are trying to compare into a square, while preserving area. After we have done that, we can just compare the side lengths of the two squares and find out which is longer. This leads us to a new form for our Main Question:
Main Question (New Form): Can we transform any shape into a square, while preserving area?
If we solve this question, then we have solved our previous Main Question with it. In fact, this sort of transformation can be done if the shape is a polygon -- meaning a shape built out of straight lines. If the shape is not a polygon, for example, a circle, then it's not as simple. Can you think of a way to transform a polygon into a square while preserving area? You should try thinking of the two questions from before as steps on the way.