The School of Mathematics
Here's a square.
Can you find a square with twice its area?

A first attempt might be doubling each side of the square.

but in fact this new square has four times the area of the original square, not two like we are looking for.
We can easily find a rectangle with twice the are of the original square

So another way of asking our question, is: Can you find a square with the same area as this rectangle?

By looking at this rectangle embedded in the larger square, we see that it has half the area of the larger square. So, yet another way of asking our question is: Can you find a square with the same area as half of the larger square?
How could we cut the larger square in half? We can cut it on the diagonal. But we are left with a triangle, not a square.
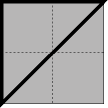
So, how could it be done?